
In a logical left shift, the bits are shifted to the left by a specified number of positions.
The leftmost bit (sign bit) is shifted out, and the vacant position on the right is filled with a zero.
Logical left shifts are primarily used for unsigned integer manipulation and simple bit operations.
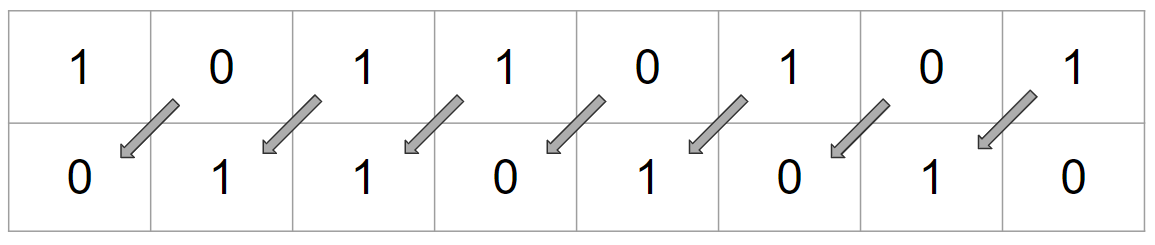
Each left shift effectively multiplies the number by 2 for each position shifted. For example, if you left-shift the binary number "00001010" by two positions, you get "00101000," which is equivalent to multiplying 00001010 by 2^2 (4).
One of the key advantages of using binary to store data is that we can perform multiplication very easily as bits are just shifted from one memory location to another.
In a right shift operation, the bits of a binary number are shifted to the right by a specified number of positions.
Similar to left shifts, new bits are introduced on the left side, and the rightmost bits are discarded. Each right shift effectively divides the number by 2 for each position shifted.
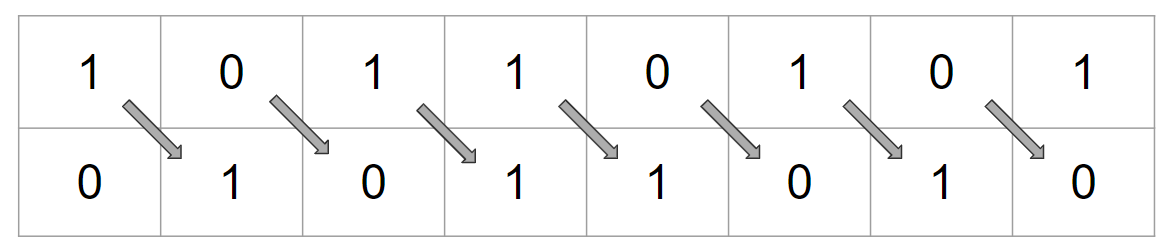
For example, if you right-shift the binary number "1010" by one position, you get "0101," which is equivalent to dividing 1010 by 2^1 (2).
Here you can see a key advantage of storing numbers in binary - division is a simple process.
What is binary shifting in computer science?