Tree traversal is the process of visiting and inspecting all the nodes of a tree data structure in a systematic order. Trees are hierarchical structures with a root node and child nodes, and tree traversal is a fundamental technique used in computer science and programming for various purposes, such as searching, printing, and manipulating data within the tree.
In-order traversal is primarily used to visit nodes in sorted order. It’s commonly employed in binary search trees (BSTs) to retrieve elements in ascending order.
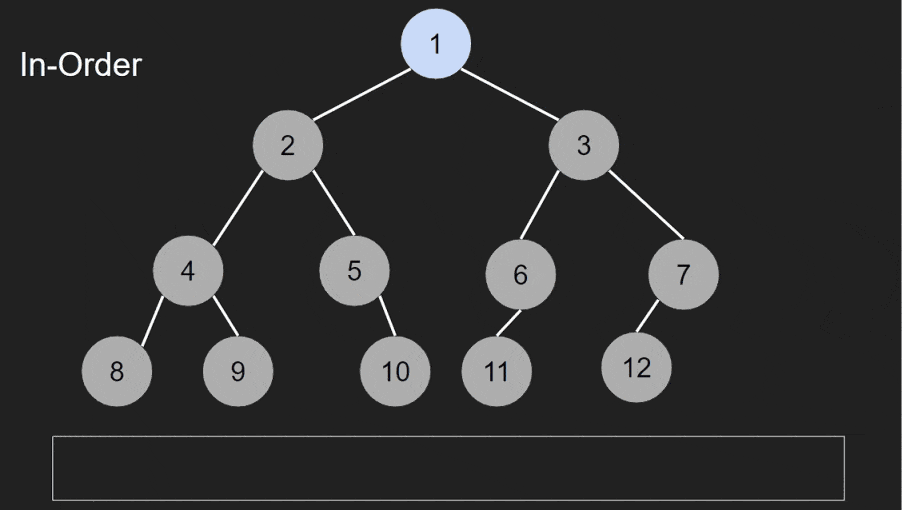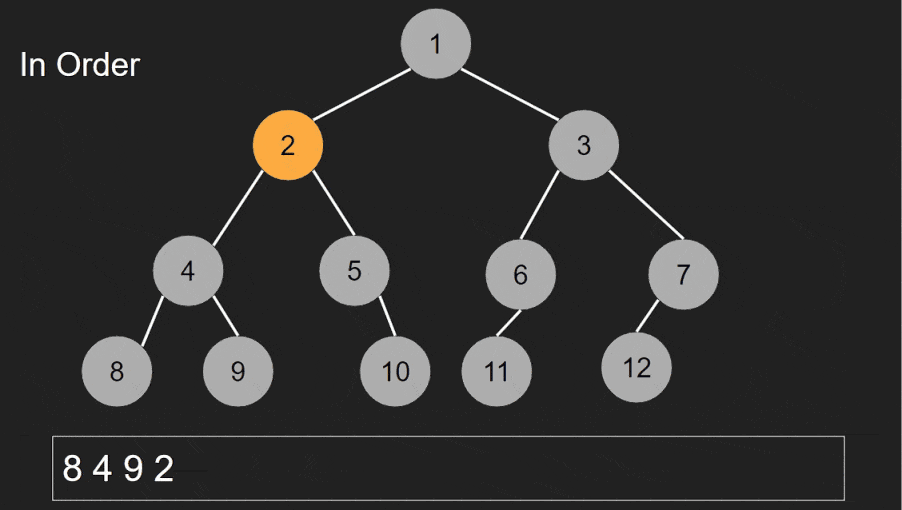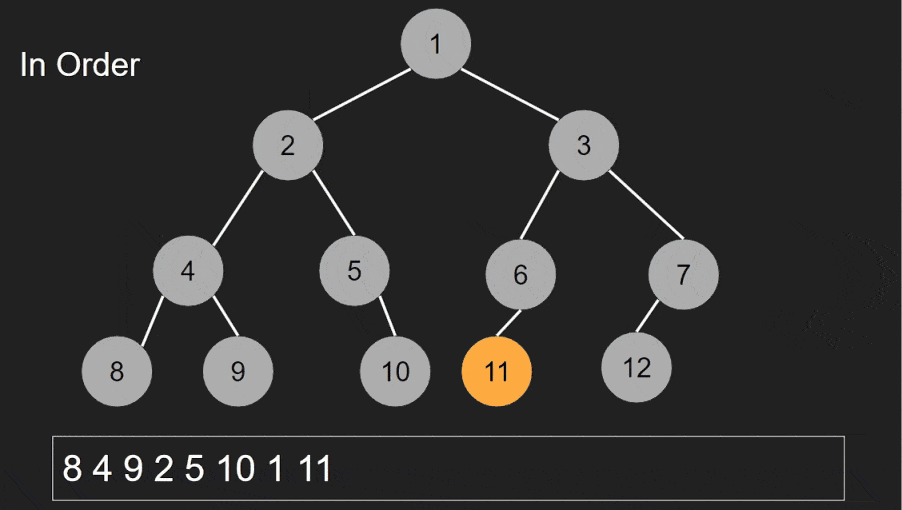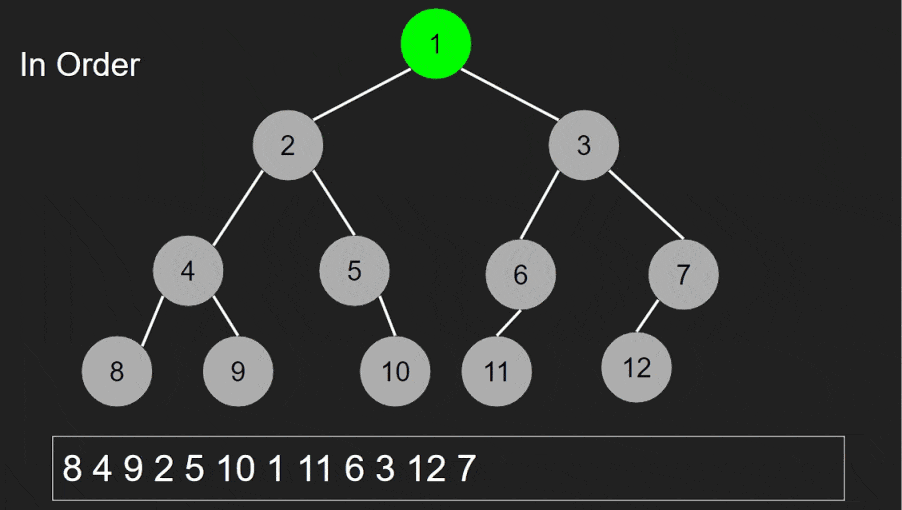
Finding elements within a binary search tree.
Constructing sorted lists from BSTs or other binary trees.
Evaluating mathematical expressions stored in expression trees.
Validating the structure of a binary tree.
Determining if a binary tree is balanced.
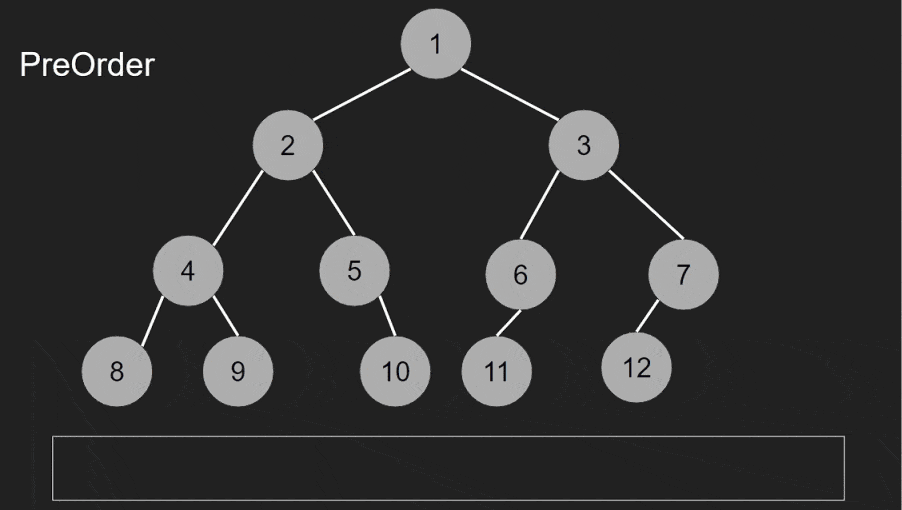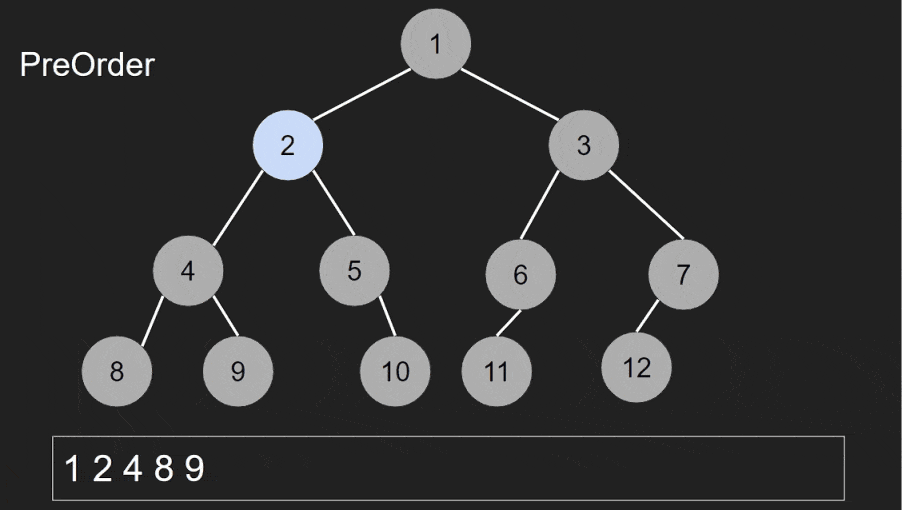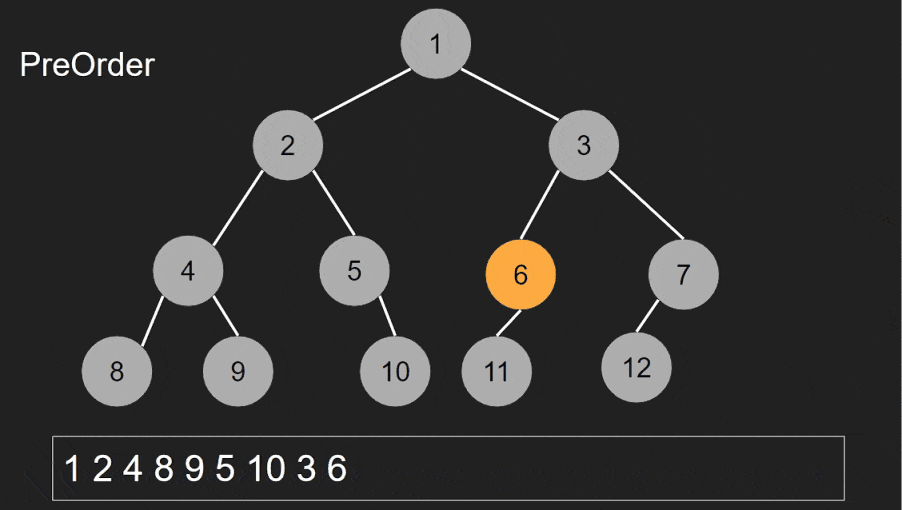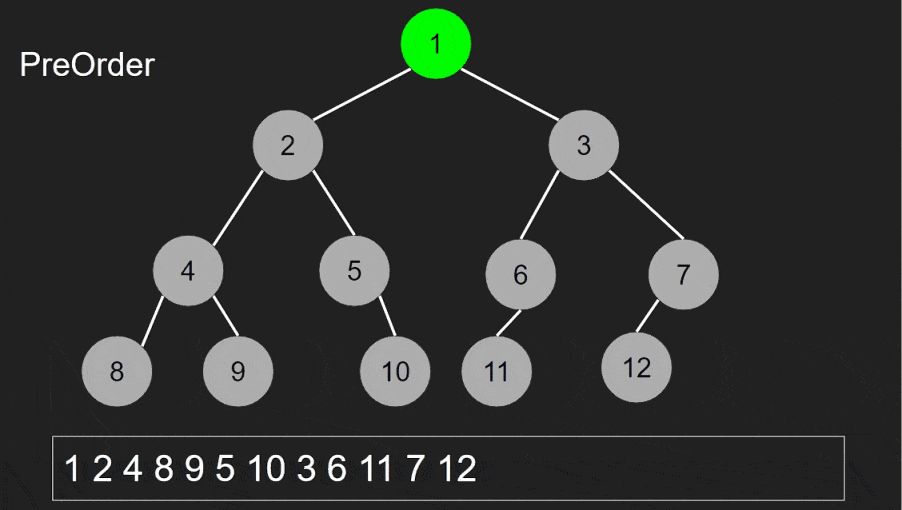
Pre-order traversal is used to perform actions on nodes before their children. It’s often used to copy a tree structure, evaluate expressions, and explore hierarchical data.
Creating a duplicate of a binary tree.
Evaluating mathematical expressions in expression trees.
Transforming an infix expression to a prefix expression (used in compilers).
Storing a tree’s structure for later reconstruction.
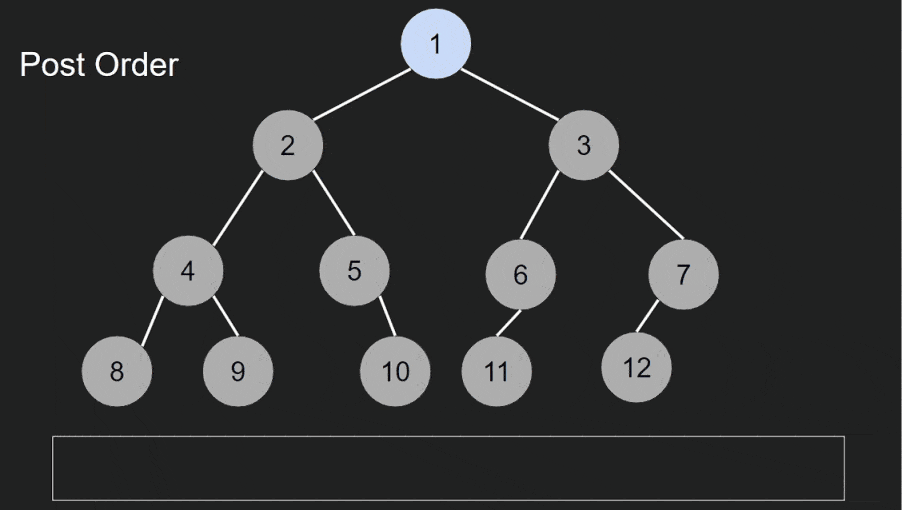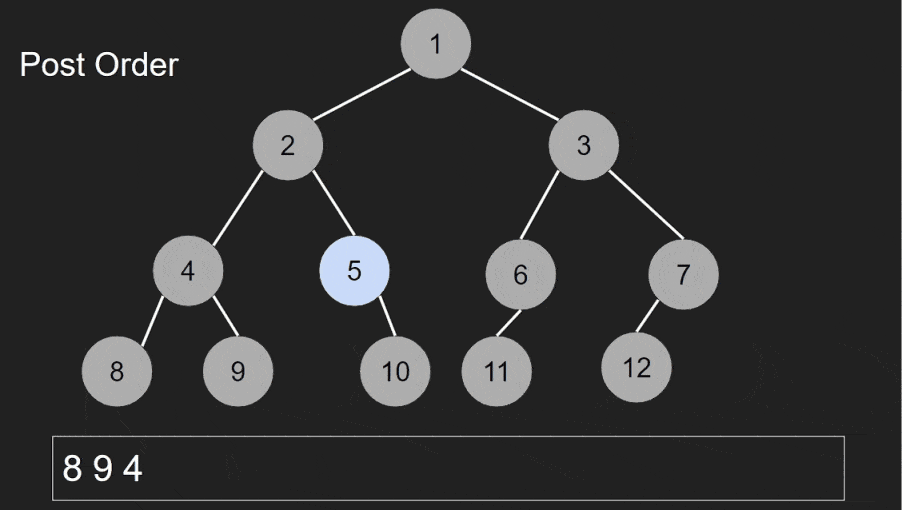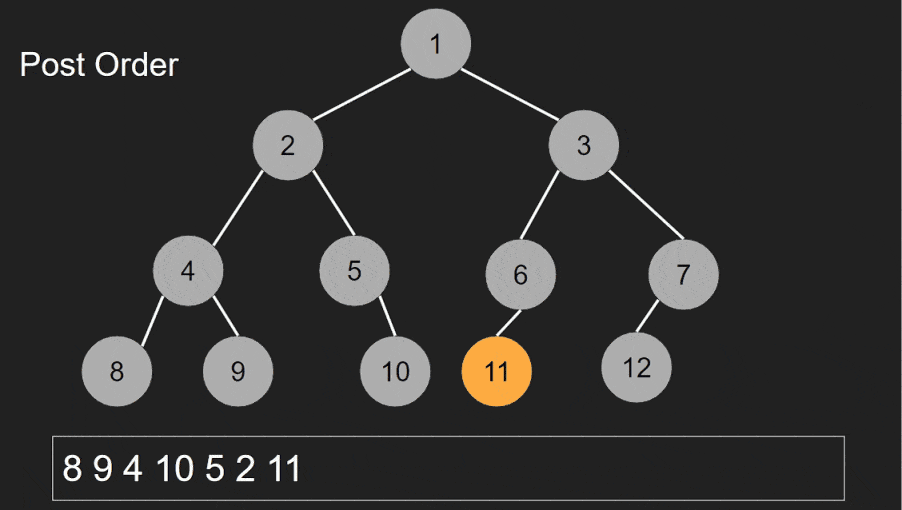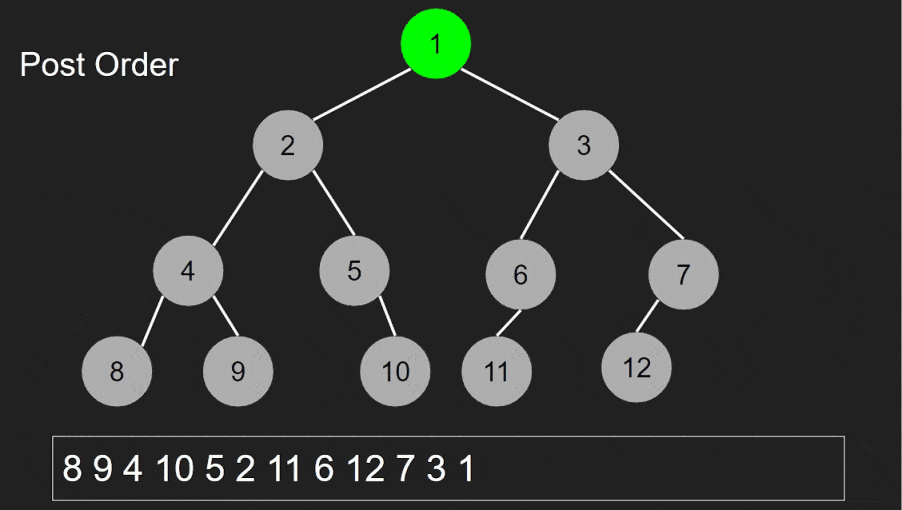
Post-order traversal is used to perform actions on nodes after their children. It’s often used in applications that require processing subtrees before the current node.
In post-order traversal, you visit the current node after its child nodes. The order is: left child, right child, current node.
Post-order traversal is often used in deleting nodes from a tree, as it ensures that child nodes are deleted before their parent nodes.
Safely removing nodes from a tree to avoid memory leaks.
Evaluating mathematical expressions in expression trees by visiting operators after their operands.
Releasing resources associated with tree nodes (used in garbage collection).
Calculating the height of a binary tree.